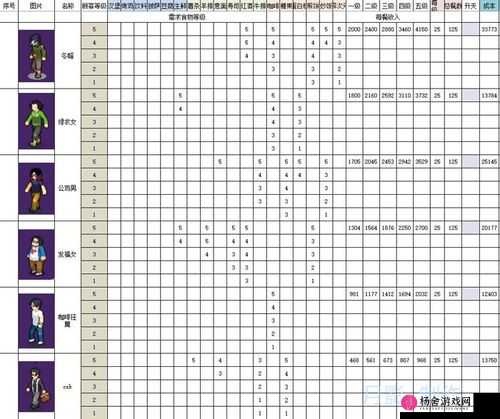
阴阳师百闻牌全面解析，金币速刷与快速获取技巧一览指南

《阴阳师百闻牌》作为一款深受玩家喜爱的卡牌收集与对战游戏，金币在游戏中扮演着至关重要的角色，无论是购买卡牌、升级角色还是参与各种活动，金币都是不可或缺的资源，掌握一些金币速刷技巧，对于玩家来说显得尤为重要，本文将详细介绍几种快速获取金币的方法，帮助玩家在游戏中更加游刃有余。

一、日常任务与签到

日常任务是获取金币的重要途径之一，在《阴阳师百闻牌》中，每日都会刷新一系列任务，包括完成一定数量的对局、参与特定模式等，这些任务不仅简单易行，而且奖励丰厚，是玩家每日必做的内容，通过完成日常任务，玩家可以轻松获得大量金币，为游戏中的各项活动提供充足的资金支持。

签到系统也是获取金币的便捷方式，玩家只需每天登录游戏，点击签到按钮，即可领取相应的奖励，签到奖励通常包括金币、卡牌碎片、道具等，随着签到天数的增加，奖励也会逐渐提升，保持每日签到的好习惯，对于积累金币来说至关重要。

二、天梯对战与匹配赛

天梯对战和匹配赛是《阴阳师百闻牌》中的核心玩法之一，也是玩家获取金币的主要途径，在天梯对战中，玩家需要与其他玩家进行实时对战，通过胜利来提升自己的天梯排名，每场胜利都会带来一定数量的金币奖励，而且随着连胜次数的增加，奖励也会相应提升，提升自己的对战技巧，争取更多的胜利，是快速获取金币的关键。

匹配赛则是一种更为休闲的对战模式，玩家可以随机匹配到其他玩家进行对战，虽然匹配赛的奖励可能不如天梯对战丰厚，但胜在门槛低、易上手，适合所有玩家参与，通过参与匹配赛，玩家不仅可以锻炼自己的对战技巧，还能获得一定数量的金币奖励。

三、周游卡与活动奖励

周游卡是《阴阳师百闻牌》中的一种特殊道具，玩家可以通过购买周游卡来获得额外的奖励，周游卡分为多个等级，每个等级都有相应的奖励池，包括金币、卡牌碎片、道具等，随着周游卡等级的提升，奖励也会越来越丰厚，对于想要快速获取金币的玩家来说，购买并升级周游卡无疑是一个明智的选择。

游戏中还会定期举办各种活动，如节日活动、限时特惠等，这些活动通常会提供大量的金币奖励，以及稀有的卡牌碎片和道具，玩家只需按照活动要求完成任务，即可领取相应的奖励，关注游戏中的各种活动，积极参与其中，是获取金币的重要途径之一。

四、热门上传阵容与互赞群

在《阴阳师百闻牌》中，玩家可以将自己组好的阵容分享上传至游戏社区，如果其他玩家使用了你的阵容并点赞，你将根据点赞数量获得相应的金币奖励，这一机制不仅鼓励了玩家之间的交流与分享，还为玩家提供了一个快速获取金币的新途径。

为了最大化这一机制的收益，玩家可以组建一个互赞群，邀请志同道合的朋友加入，在互赞群中，大家可以互相分享自己的阵容，并相互点赞，从而快速提升点赞数量，获得更多金币奖励，需要注意的是，官方并未设置点赞数量的上限，因此这一方法具有极高的潜力。

五、成就奖励与兑换码

成就系统是《阴阳师百闻牌》中的一个重要功能，玩家通过完成特定的成就任务，可以获得丰厚的奖励，包括金币、卡牌碎片等，这些成就任务通常与游戏进度、对战表现等密切相关，因此玩家在享受游戏乐趣的同时，也能不断解锁新的成就，获得额外的金币奖励。

游戏中还会定期发布一些兑换码，玩家可以通过输入兑换码来获得相应的奖励，这些兑换码通常会在游戏官网、社交媒体等渠道发布，玩家需要密切关注这些渠道，以便及时获取并使用兑换码，通过兑换码获得的奖励往往包括金币、卡牌等珍贵资源，对于玩家来说无疑是一个额外的惊喜。

结尾问题与解答

问题一：如何在《阴阳师百闻牌》中快速获取大量金币？

解答：在《阴阳师百闻牌》中，快速获取大量金币的方法有多种，玩家可以通过完成日常任务、参与天梯对战和匹配赛来获取金币，购买并升级周游卡也是获取金币的有效途径，关注游戏中的各种活动，积极参与其中，也能获得大量的金币奖励，玩家还可以利用热门上传阵容与互赞群机制，通过分享阵容并相互点赞来获取金币。

问题二：周游卡在《阴阳师百闻牌》中有什么作用？

解答：周游卡在《阴阳师百闻牌》中是一种特殊道具，玩家可以通过购买周游卡来获得额外的奖励，周游卡分为多个等级，每个等级都有相应的奖励池，包括金币、卡牌碎片、道具等，随着周游卡等级的提升，奖励也会越来越丰厚，购买并升级周游卡可以帮助玩家快速获取大量金币和其他珍贵资源。

问题三：如何在游戏中利用热门上传阵容与互赞群机制获取金币？

解答：在《阴阳师百闻牌》中，玩家可以将自己组好的阵容分享上传至游戏社区，如果其他玩家使用了你的阵容并点赞，你将根据点赞数量获得相应的金币奖励，为了最大化这一机制的收益，玩家可以组建一个互赞群，邀请志同道合的朋友加入，在互赞群中，大家可以互相分享自己的阵容，并相互点赞，从而快速提升点赞数量，获得更多金币奖励，需要注意的是，官方并未设置点赞数量的上限，因此这一方法具有极高的潜力。